Publications
ResCP: Residual Conformal Prediction for Time Series Forecasting
ICLR 2026

We propose ResCP, a novel conformal prediction method for time series forecasting. ResCP leverages the efficiency and representation capabilities of Reservoir Computing to dynamically reweight conformity scores at each time step. This allows us to account for local temporal dynamics when modeling the error distribution without compromising computational scalability. Moreover, we prove that, under reasonable assumptions, ResCP achieves asymptotic conditional coverage.
@misc{neglia2025rescp,
title = {ResCP: Residual Conformal Prediction for Time Series Forecasting},
author = {Neglia, Roberto and Cini, Andrea and Bronstein, Michael M. and Bianchi, Filippo Maria},
year = {2025},
eprint = {2510.05060},
archivePrefix = {arXiv},
primaryClass = {cs.LG},
url = {https://arxiv.org/abs/2510.05060},
}
Bridging Theory and Practice in Link Representation with Graph Neural Networks
NeurIPS 2025 (spotlight)
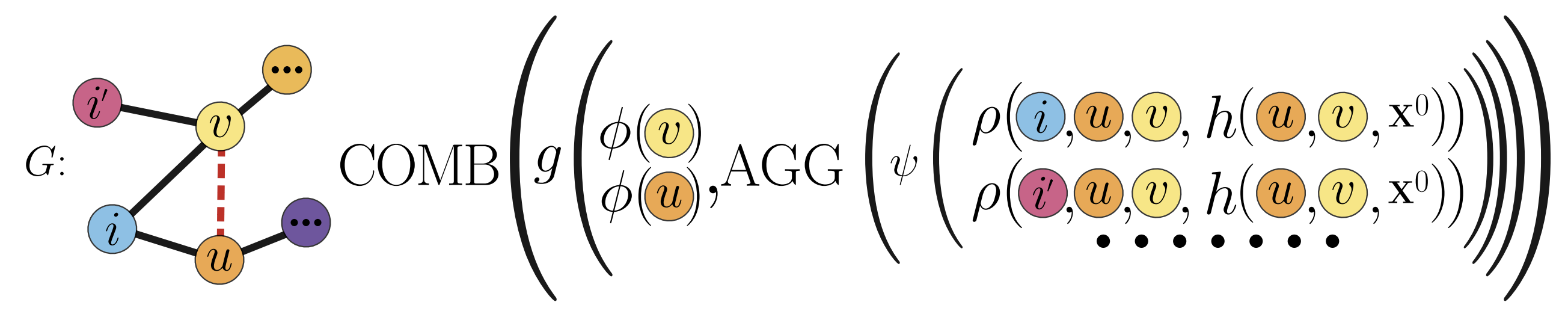
We introduce a unifying framework that subsumes existing message-passing link models and enables formal expressiveness comparisons. Using this framework, we derive a hierarchy of state-of-the-art methods and offer theoretical tools to analyze future architectures. To complement our analysis, we propose a synthetic evaluation protocol comprising the first benchmark specifically designed to assess link-level expressiveness.
@misc{lachi2025bridgingtheorypracticelink,
title={Bridging Theory and Practice in Link Representation with Graph Neural Networks},
author={Veronica Lachi and Francesco Ferrini and Antonio Longa and Bruno Lepri and Andrea Passerini and Manfred Jaeger},
year={2025},
eprint={2506.24018},
archivePrefix={arXiv},
primaryClass={cs.LG},
url={https://arxiv.org/abs/2506.24018},
}
Torch Geometric Pool: the Pytorch library for pooling in Graph Neural Networks

We present Torch Geometric Pool (TGP), a PyTorch library that implements a wide variety of graph pooling methods for GNNs. TGP is designed with an easy-to-use API, enabling seamless integration with existing PyTorch Geometric codebases. The library includes implementations of state-of-the-art pooling techniques, along with comprehensive documentation and examples to facilitate adoption by the research community.
@misc{bianchi2025torchgeometricpoolpytorch,
title={Torch Geometric Pool: the Pytorch library for pooling in Graph Neural Networks},
author={Filippo Maria Bianchi and Carlo Abate and Ivan Marisca},
year={2025},
eprint={2512.12642},
archivePrefix={arXiv},
primaryClass={cs.LG},
url={https://arxiv.org/abs/2512.12642},
}
Efficient Learning of Molecular Properties Using Graph Neural Networks Enhanced with Chemistry Knowledge
Journal ACS Omega
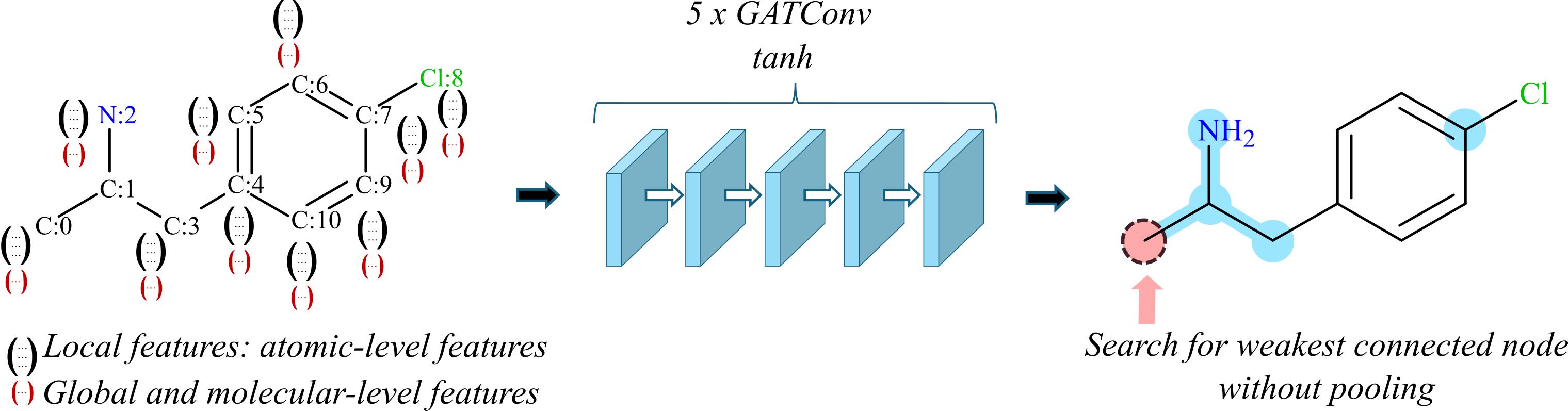
We build a simple GNN-based model that integrates chemistry knowledge that GNNs may have difficulties to learn. We show that this combination greatly enhances the accuracy compared with the pure GNN approach. With a simple approach, this study highlights some limitations of GNNs and the crucial benefit of giving GNN models easy access to global information about the graph in the context of applications to chemistry. We focus on regression tasks at the molecular level, on small-molecule data sets.
@article{doi:10.1021/acsomega.5c07178,
author = {Lutchyn, Tetiana and Mardal, Marie and Ricaud, Benjamin},
title = {Efficient Learning of Molecular Properties Using Graph Neural Networks Enhanced with Chemistry Knowledge},
journal = {ACS Omega},
volume = {10},
number = {45},
pages = {54421-54429},
year = {2025},
doi = {10.1021/acsomega.5c07178},
URL = {https://doi.org/10.1021/acsomega.5c07178},
eprint = {https://doi.org/10.1021/acsomega.5c07178}
}
On Time Series Clustering with Graph Neural Networks
TMLR 2025
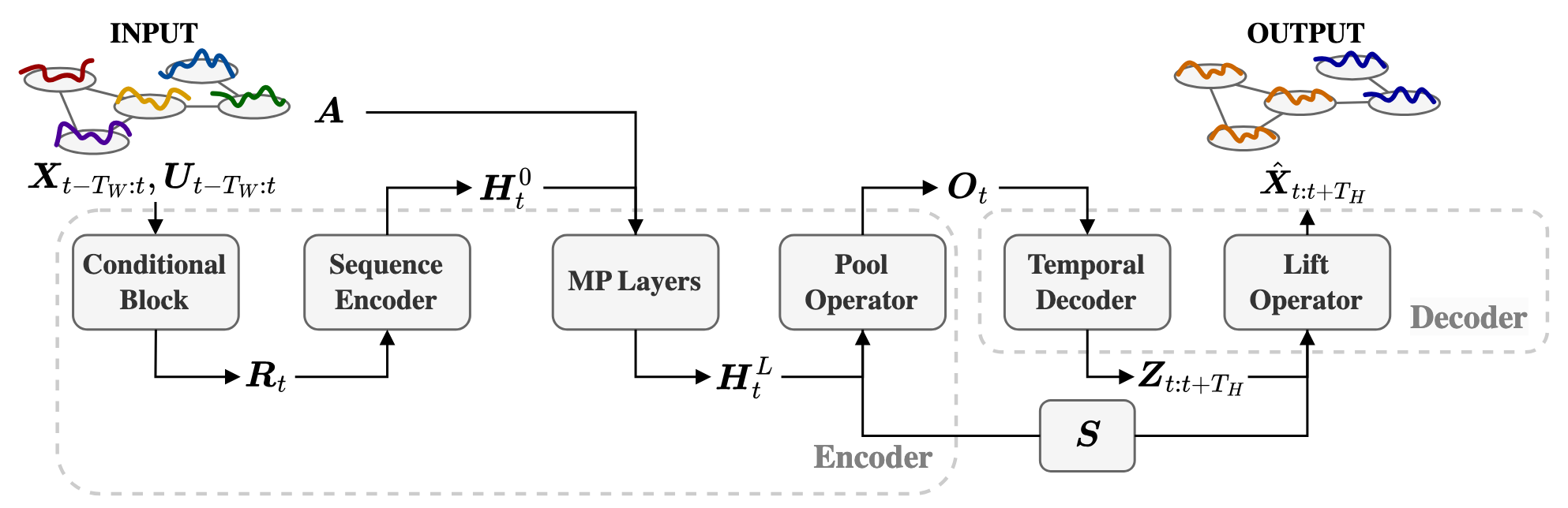
We study the effectiveness of Spatio-temporal Graph Neural Networks to perform clustering of time series, whose dependencies are represented by a graph.
@article{hansen2025clustering,
title = {On Time Series Clustering with Graph Neural Networks},
author = {Hansen, Jonas Berg and Cini, Andrea and Bianchi, Filippo Maria},
journal = {Transactions on Machine Learning Research},
issn = {2835-8856},
year = {2025},
url = {https://openreview.net/forum?id=MHQXfiXsr3}
}
Relational Conformal Prediction for Correlated Time Series
ICML 2025
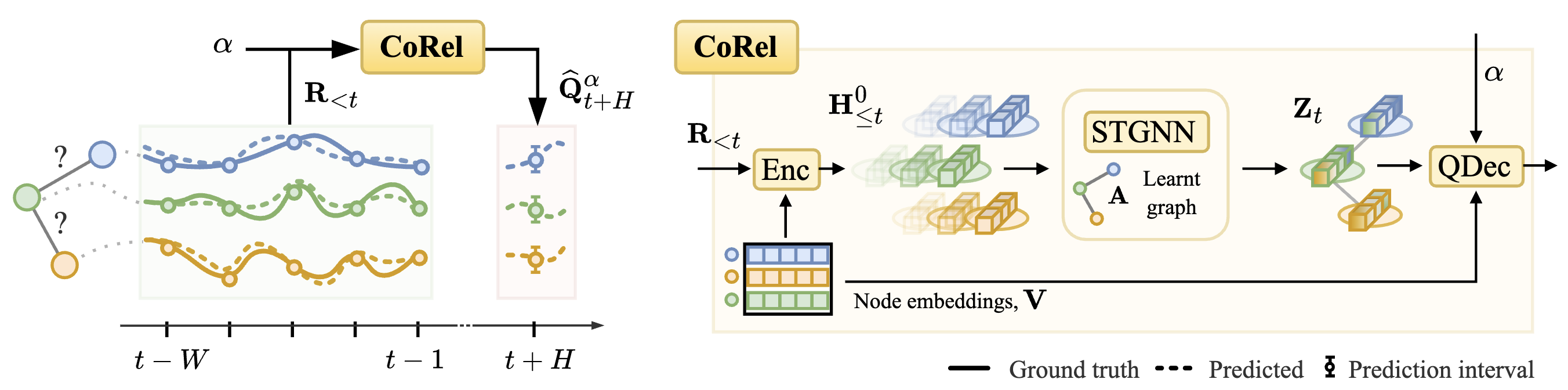
We propose a novel conformal prediction method based on graph deep learning. Our method can be applied on top of any time series predictor, can learn the relationships across the time series and, thanks to an adaptive component, can handle non-exchangeable data and nonstationarity in the time series.
@inproceedings{cini2025relational,
title = {Relational Conformal Prediction for Correlated Time Series},
author = {Cini, Andrea and Jenkins, Alexander and Mandic, Danilo and Alippi, Cesare and Bianchi, Filippo Maria},
booktitle = {Proceedings of the 42nd International Conference on Machine Learning},
year = {2025},
series = {Proceedings of Machine Learning Research},
publisher = {PMLR}
}
BN-Pool: a Bayesian Nonparametric Approach to Graph Pooling
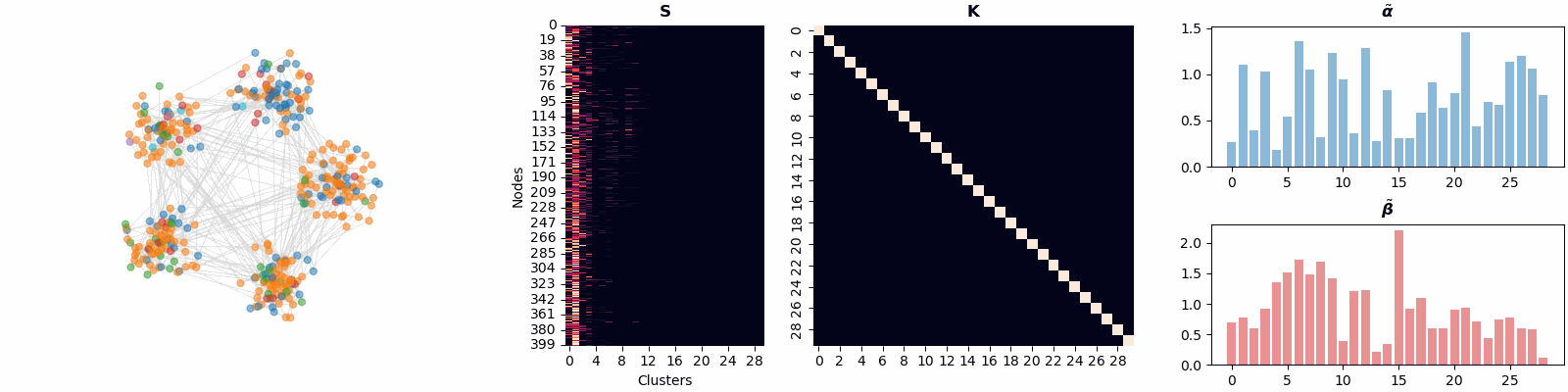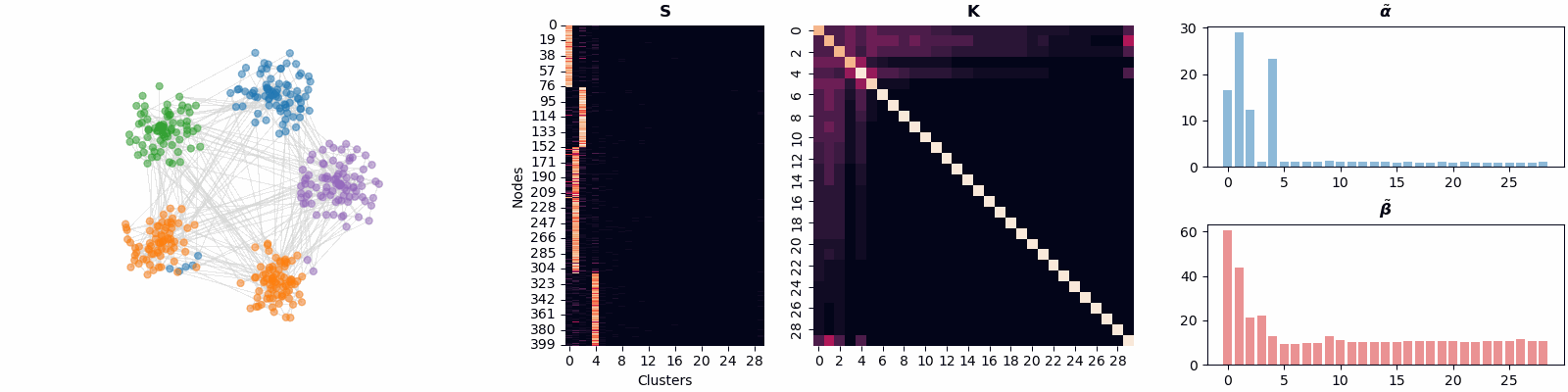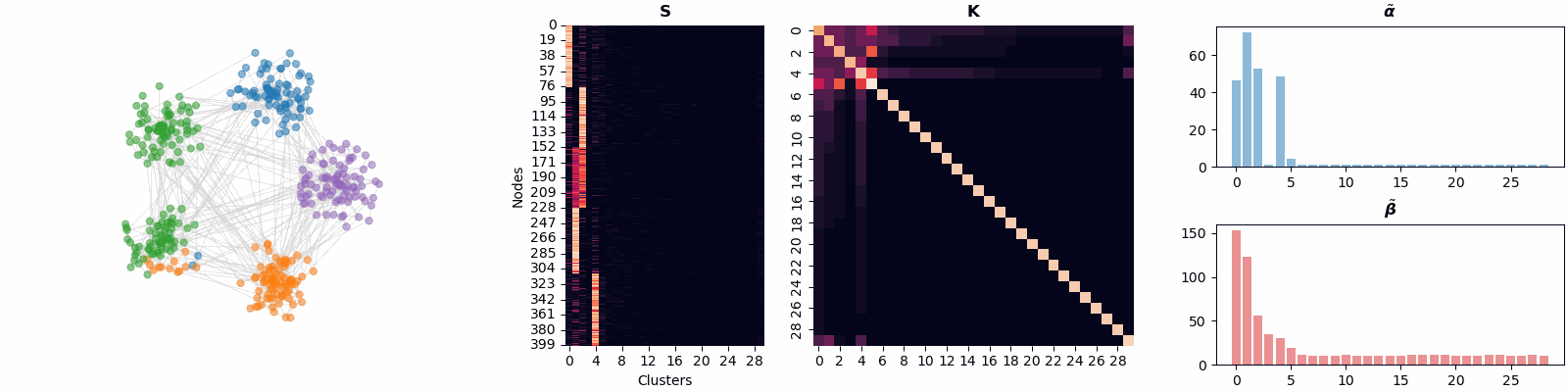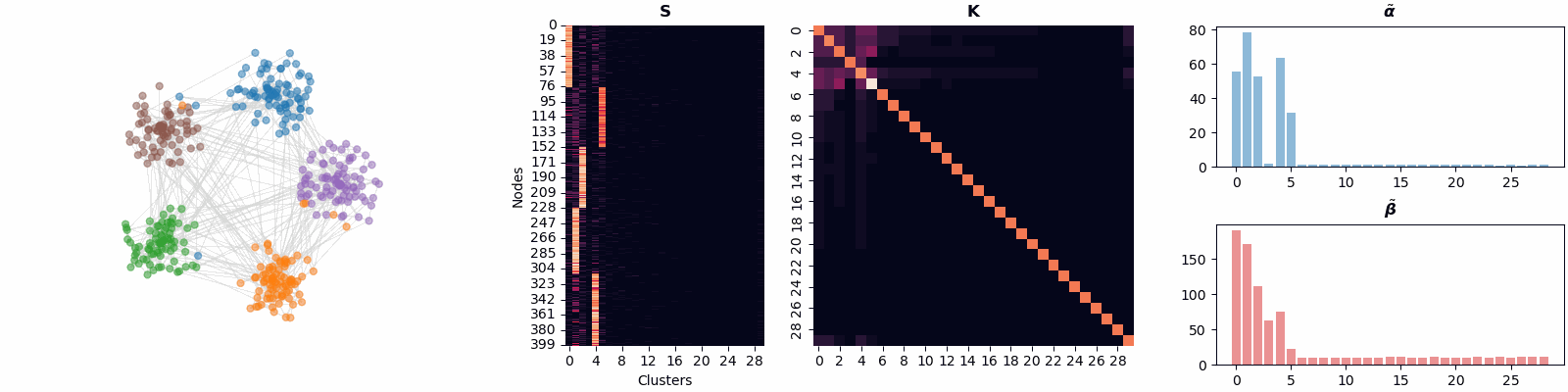
We introduce BN-Pool, the first clustering-based pooling method for GNNs that adaptively determines the number of supernodes in the pooled graph. This is done by partitioning the graph nodes into an unbounded number of clusters using a generative model based on a Bayesian non-parametric framework.
@misc{castellana2025bnpool,
title = {BN-Pool: a Bayesian Nonparametric Approach to Graph Pooling},
author = {Daniele Castellana and Filippo Maria Bianchi},
year = {2025},
eprint = {2501.09821},
archivePrefix = {arXiv},
primaryClass = {cs.LG},
url = {https://arxiv.org/abs/2501.09821},
}
Interpreting Temporal Graph Neural Networks with Koopman Theory

We propose an XAI technique based on Koopman theory to interpret temporal graphs and the spatio-temporal Graph Neural Newtworks used to process them. The proposed approach allows to identify nodes and time steps when relevant events occur.
@misc{guerra2024interpretingtemporalgraphneural,
title = {Interpreting Temporal Graph Neural Networks with Koopman Theory},
author = {Michele Guerra and Simone Scardapane and Filippo Maria Bianchi},
year = {2024},
eprint = {2410.13469},
archivePrefix = {arXiv},
primaryClass = {cs.LG},
}
MaxCutPool: differentiable feature-aware Maxcut for pooling in graph neural networks
ICLR 2025
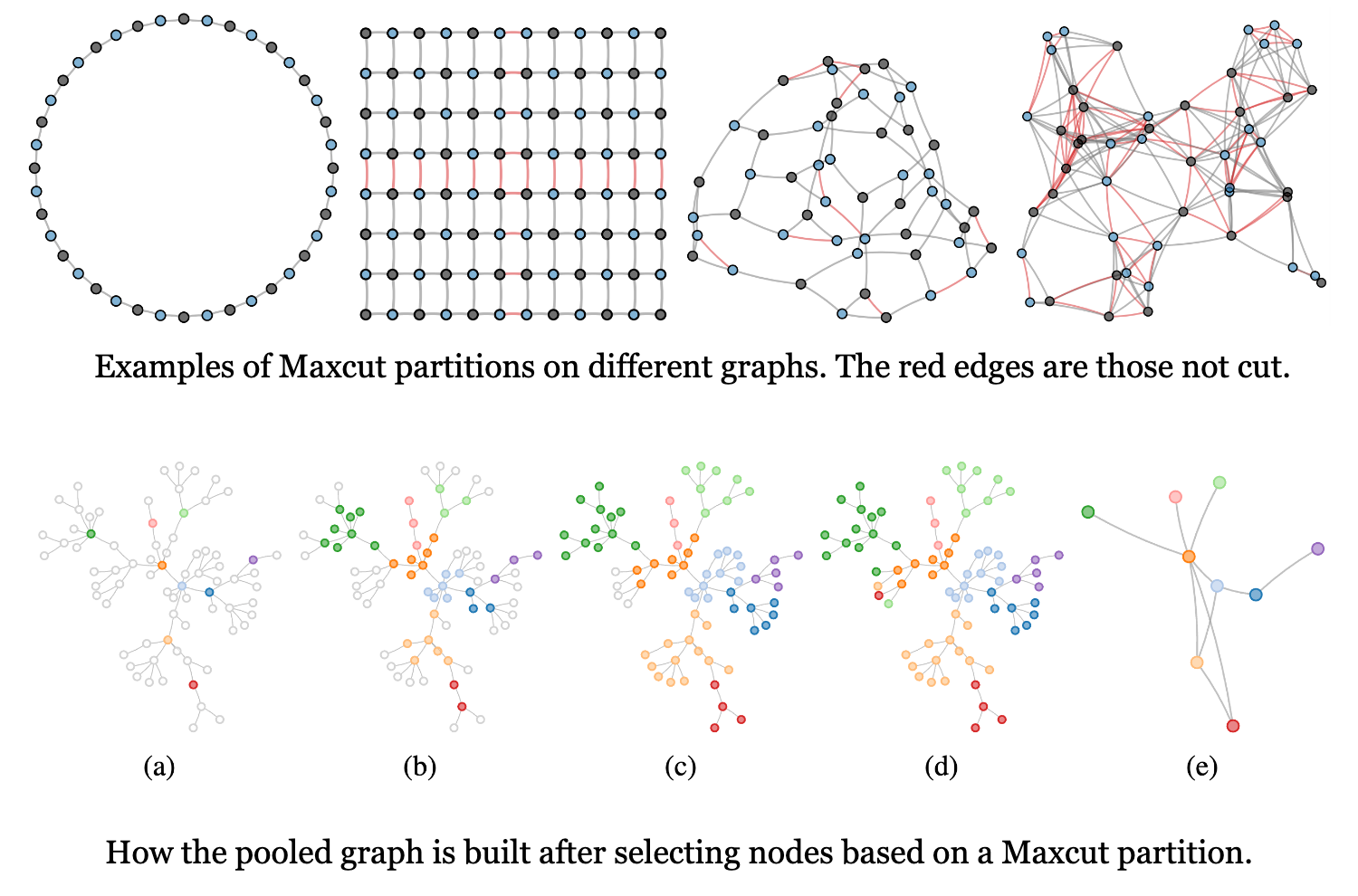
We propose a novel approach to compute the MAXCUT in attributed graphs, i.e., graphs with features associated with nodes and edges. Our approach is robust to the underlying graph topology and is fully differentiable, making it possible to find solutions that jointly optimize the MAXCUT along with other objectives. Based on the obtained MAXCUT partition, we implement a hierarchical graph pooling layer for Graph Neural Networks, which is sparse, differentiable, and particularly suitable for downstream tasks on heterophilic graphs.
@inproceedings{abate2025maxcutpool,
title = {MaxCutPool: differentiable feature-aware Maxcut for pooling in graph neural networks},
author = {Carlo Abate and Filippo Maria Bianchi},
booktitle = {The Thirteenth International Conference on Learning Representations},
year = {2025},
url = {https://openreview.net/forum?id=xlbXRJ2XCP}
}
Graph-based Forecasting with Missing Data through Spatiotemporal Downsampling
ICML 2024
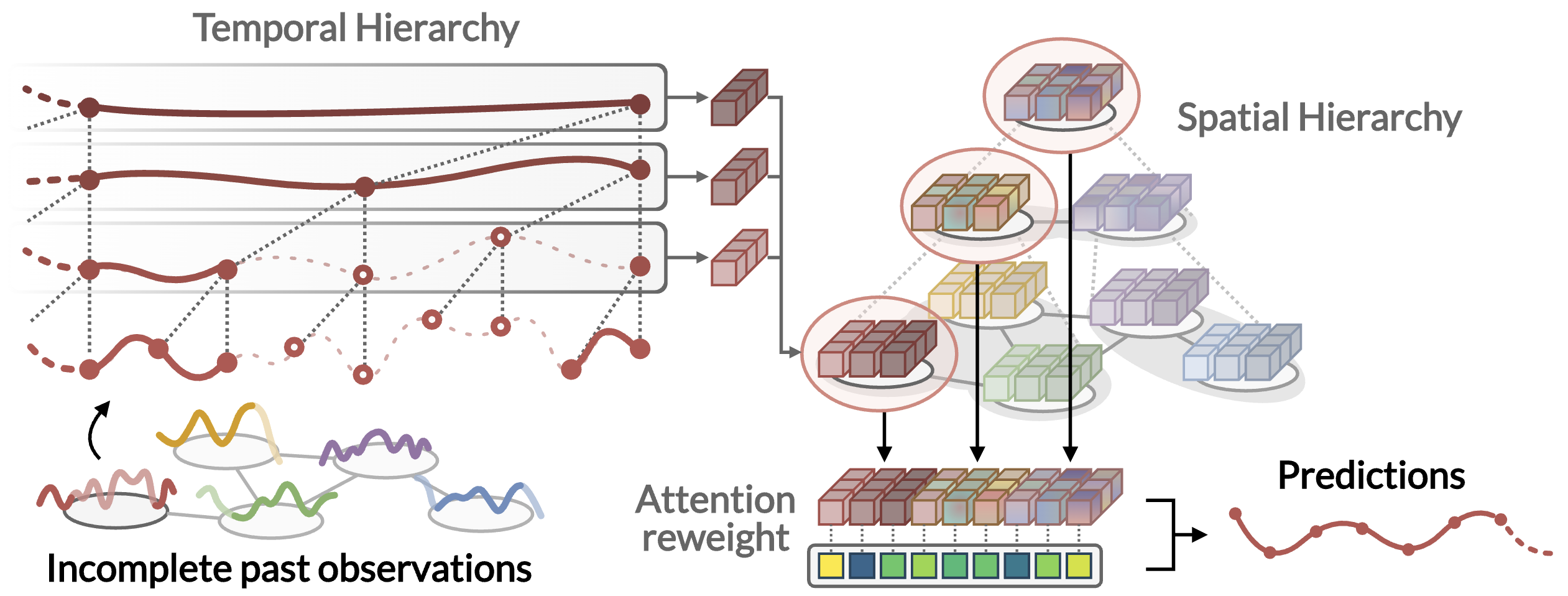
Spatiotemporal graph neural networks achieve striking results by representing the relationships across time series as a graph. Nonetheless, most existing methods rely on the often unrealistic assumption that inputs are always available and fail to capture hidden spatiotemporal dynamics when part of the data is missing. In this work, we tackle this problem through hierarchical spatiotemporal downsampling. The input time series are progressively coarsened over time and space, obtaining a pool of representations that capture heterogeneous temporal and spatial dynamics. Conditioned on observations and missing data patterns, such representations are combined by an interpretable attention mechanism to generate the forecasts.
@inproceedings{marisca2024graph,
title = {Graph-based Forecasting with Missing Data through Spatiotemporal Downsampling},
author = {Marisca, Ivan and Alippi, Cesare and Bianchi, Filippo Maria},
booktitle = {Proceedings of the 41st International Conference on Machine Learning},
pages = {34846--34865},
year = {2024},
volume = {235},
series = {Proceedings of Machine Learning Research},
publisher = {PMLR}
}
The expressive power of pooling in Graph Neural Networks
NeurIPS 2023
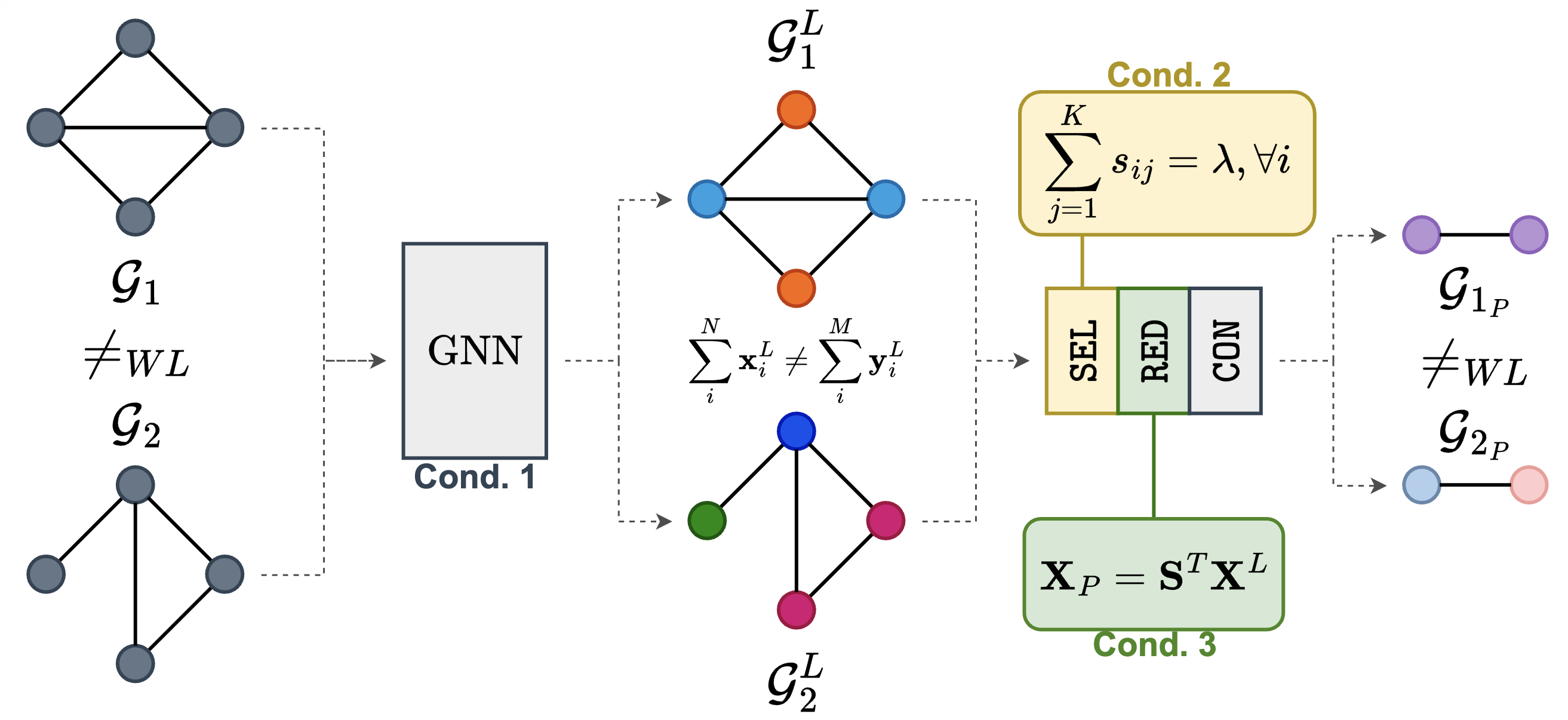
A graph pooling operator can be expressed as the composition of 3 functions: SEL defines how to form the vertices of the coarsened graph; RED computes the vertex features in the coarsened graph; CON computes the edges in the coarsened graphs. In this work we show that if certain conditions are met on the GNN layers before pooling, on the SEL, and on the RED functions, then enough information is preserved in the coarsened graph. In particular, if two graphs are WL-distinguishable, their coarsened versions will also be WL-dinstinguishable.
@article{bianchi2023expressive,
title = {The expressive power of pooling in Graph Neural Networks},
author = {Filippo Maria Bianchi and Veronica Lachi},
journal = {Advances in neural information processing systems},
volume = {36},
year = {2023}
}
Total Variation Graph Neural Networks
ICML 2023
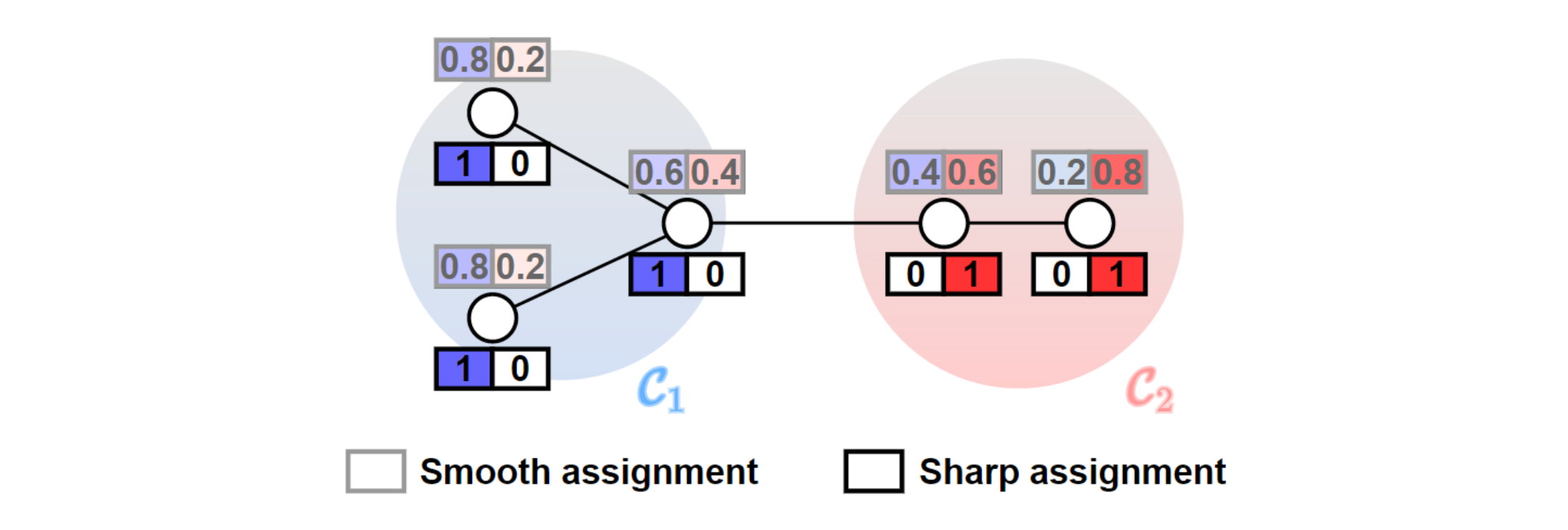
We propose the Total Variation GNN model, which can be used to cluster the vertices of an annotated graph, by accounting both for the graph topology and the vertex features. Compared to other GNNs for clustering, TVGNN creates sharp cluster assignments that better approximate the optimal (in the minimum cut sense) partition. The TVGNN model can also be used to implement graph pooling in a deep GNN architecture for tasks such as graph classification.
@inproceedings{hansen2023tvgnn,
title = {Total Variation Graph Neural Networks},
author = {Hansen, Jonas Berg and Bianchi, Filippo Maria},
booktitle = {Proceedings of the 40th international conference on Machine learning},
year = {2023},
organization = {ACM}
}
Scalable Spatiotemporal Graph Neural Networks
AAAI 2023
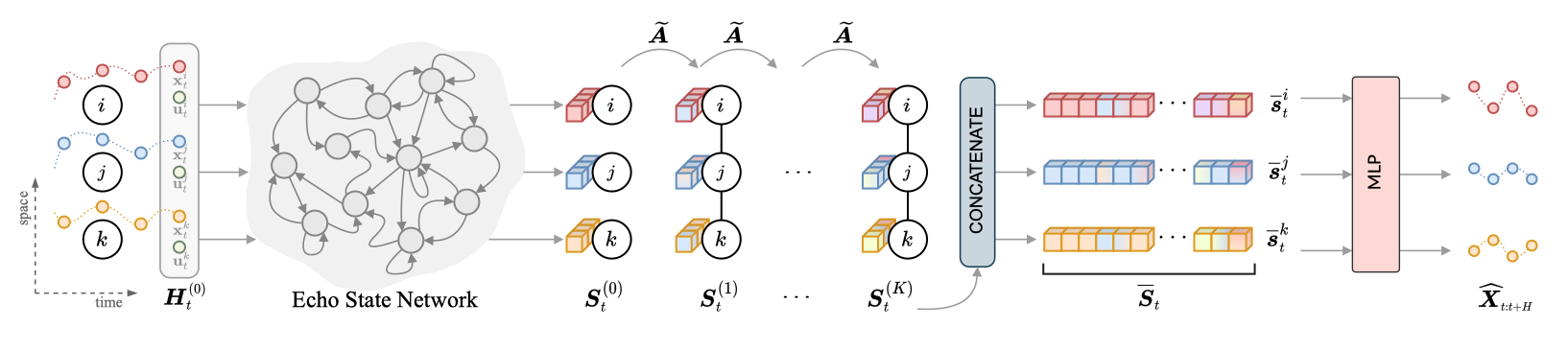
SGP is novel approach based on an encode-decoder architecture with a training-free spatiotemporal encoding scheme and where the only learned parameters are in the node-level trainable decoder (an MLP). Representations for each point in time and space can be precomputed and the decoder can be trained by sampling uniformly time and space thus gettig rid of the dependency on sequence lenght and graph size for what concerns the computational complexity of the training procedure. The spatiotemporal encoder relies on two modules: 1) a randomized recurrent neural network for encoding sequences and 2) a propagation process through the graph structure exploiting powers of a graph shift operator.
@article{cini2023scalable,
title = {Scalable Spatiotemporal Graph Neural Networks},
author = {Cini, Andrea and Marisca, Ivan and Bianchi, Filippo Maria and Alippi, Cesare},
journal = {Proceedings of the 37th AAAI Conference on Artificial Intelligence},
year = {2023}
}